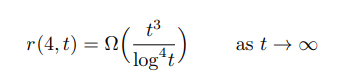Hoe los je een wiskundig probleem op waar al veertig jaar geen vooruitgang in is geboekt? Dr. Sam Mattheus, verbonden aan de Vrije Universiteit Brussel, vertrok voor een jaar naar de Verenigde Staten om het uit te zoeken. Hij combineerde zijn kennis over de eindige meetkunde met de klassieke grafentheorie en loste niet alleen een decennia oud probleem op, maar biedt een innoverend alternatief voor de huidige aanpak van Ramsey-problemen. “Ook om andere Ramsey-getallen te berekenen, kan de eindige meetkunde hopelijk oplossingen bieden”, zegt Mattheus.
Het vraagstuk dat Mattheus oploste, kadert binnen de zogenaamde Ramsey-getallen. Dat zijn fundamentele grootheden die de grenzen van mogelijke wanorde weergeven. Ze zijn vooral notoir moeilijk te berekenen. Toch slaagde Mattheus er na enkele maanden al in, in samenwerking met prof. Jacques Verstraete van de University of California San Diego (UCSD). “Het was voor ons ook een grote verrassing”, zegt Mattheus. “Het was lange tijd niet duidelijk hoe we het gingen aanpakken en of het überhaupt zou lukken.” Op een dag wandelde Mattheus het bureau van Verstraete binnen met een idee. Na een paar uur filosoferen gingen ze aan de slag. Uiteindelijk zouden ze op slechts enkele maanden tijd een oplossing vinden voor het specifieke Ramsey-probleem: r(4,t).
Mattheus behaalde in 2022 zijn doctoraat aan de VUB binnen de eindige meetkunde. Hij overtuigde de Belgian American Educational Foundation en het beurzenprogramma Fulbright om zijn onderzoek over de Ramsey-theorie te financieren en vertrok naar de Verenigde Staten met een plan. “Ik liep al enkele jaren rond met het idee om de eindige meetkunde te betrekken bij het berekenen van Ramsey-getallen,” zegt Mattheus. In de VS werkt hij momenteel als gastonderzoeker aan de USCD onder leiding van Verstraete. De samenwerking met Verstraete is geen toeval. “Prof. Verstraete schreef eerder met prof. Dhruv Mubayi van de University of Illinois de paper die mij inspireerde een geometrisch perspectief te gebruiken om een van de Ramsey-vraagstukken op te lossen.”
Het idee was er, maar de uitvoering ontbrak nog. De grafentheorie is de klassieke manier om Ramsey-getallen te berekenen, Mattheus voegde daar zijn eigen kennis aan toe. Met de Hermitische kromme, een bekend object uit de eindige meetkunde, vond Mattheus de sleutel om het probleem r(4,t) op te lossen. “Het was een kwestie van twee domeinen, de eindige meetkunde en de grafentheorie, te combineren”, zegt Mattheus. “De nodige kennis bestond al, maar de ideeën waren nog niet bij elkaar gebracht. Het draaide om the right place and the right time. We pleiten zo eigenlijk voor meer kruisbestuiving binnen de wiskunde. Ook om andere Ramsey-getallen te berekenen, kan de eindige meetkunde hopelijk oplossingen bieden.”
Maar hoe voelt het om een wiskundig probleem op te lossen dat decennia oud is? “Vooral de reactie vanuit de ‘grafentheorie-gemeenschap’ is surreëel", zegt Mattheus. "Een dag nadat we het bewijs online plaatsten, kreeg ik al een telefoontje. Of ik een week later op een congres over het bewijs kon komen spreken. Ik mag binnenkort ook een lezing geven in China.” Mattheus behaalde zijn doctoraat pas in 2022, maar plots gaat het snel. “Toen iemand als Timothy Gowers erover tweette en vertelde hoe hij zelf nog geprobeerd had om het probleem op te lossen, moest ik toch even slikken.” Gowers kreeg in 1998 de Fields Medal, zeg maar de Nobelprijs voor wiskundigen onder de 40 jaar oud.
In oktober keert Mattheus terug naar de vakgroep Wiskunde en Data Science aan de VUB met een beurs van het Fonds Wetenschappelijk Onderzoek - Vlaanderen. “Ik kijk er naar uit om met mijn rugzak vol problemen terug te keren naar Brussel en samen met mijn collega’s verder te werken aan de Ramsey-theorie.”
Ramsey-theorie
Ramsey-problemen gaan over hoelang het duurt voor er in wanorde patronen ontstaan. Ze maken deel uit van de combinatieleer, waarbij wiskundigen kijken naar verzamelingen van objecten. Er bestaan een hele reeks onopgeloste Ramsey-problemen. Een voorbeeld dat wel al opgelost is, is r(4, 5) = 25. Als we de metafoor van een feestje gebruiken met kennissen en onbekenden, nodig je in dat geval 25 mensen uit. Volgens het Ramsey-getal zal er dan een groepje bestaan met vier wederzijdse kennissen of een groepje met vijf vreemden. Wil je die samenstellingen voorkomen, mag je maar 24 mensen uitnodigen. Met 24 genodigden zou het mogelijk zijn om een samenstelling te bekomen waar geen groepje met vier kennissen of vijf vreemden aanwezig is. In de wiskunde gebruiken ze ook de termen rode kliek en blauwe kliek om de twee groepen te beschrijven. Wat het maximaal aantal genodigden is om vier wederzijdse kennissen (rode kliek) of zes vreemden (blauwe kliek) te vermijden, weet nog steeds niemand. Dr. Mattheus zette de rode kliek vast op 4 en onderzocht wat er met het Ramsey-getal gebeurde naarmate de blauwe kliek groter werd. In wiskundetaal ziet het resultaat van Mattheus en Verstraete er dan als volgt uit: